There are ways of knowing.
There are ways of knowing that bypass, if not the brain, then at least the logical, linear, linguistic parts of the brain. There are ways of knowing things with your hands. There are ways of demonstrating ideas because you can use them, or do them, or at least make a model of them.
 |
| A crocheted mathematical model of a coral reef. crochetcoralreef.org |
There are women who make models of coral by crocheting [Margaret and Christine Wertheim, The Coral Reef Project]. They are able to demonstrate that in the seemingly-random shapes of coral, there is logic. There is order. There is an unwritable formula. In the organic, frilly shapes of corals are embedded straight lines. And they can prove it because they can make it with their hands, manipulate it, fold it, and hold it up or hand it over for anybody else to experience. To my understanding, nobody has been able to reduce this geometry to an equation; although they can reduce it to a pattern. (Eg. “Crochet three, increase one.”)
There is truth in the things we can make and demonstrate with our hands, even if we can’t reduce it to a formula.
As Margaret Wertheim, co-founder of the Coral Reef Project, says: “I can see it. I can feel it. I can touch it. I can play with it.” We can "literally, physically play with ideas.”
___________________________________
There are ways of knowing.
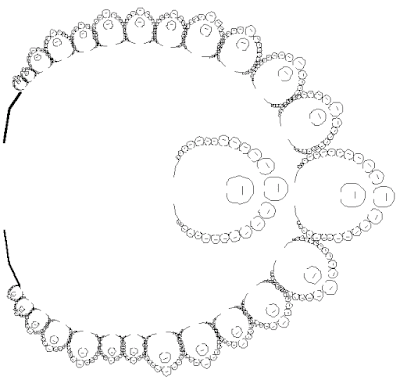 |
| Ron Eglash. Drawing of the plan of a Ba-Ila village in Africa, created using fractal geometry. |
There are villagers all over Africa who build their villages in fractal patterns ; not the same fractal pattern, but many different ones across the continent [Ron Eglash, Rensselaer Polytechnic Institute]. I don’t pretend to understand the math or the science of fractals, but I know it refers to a geometry which replicates the same shape at different scales, ad infinitum. Without equations or labels or formulae, Africans have been building communities using fractal geometry for centuries; expressing their social structures and embedding their myths in their architecture. There is a non-hierarchical way of knowing the world which is reflected in how they order their communities.
There are parts of their processes that are quite possibly the earliest visual representations of binary code. (I don’t begin to understand.)
There are ways of knowing.
____________________________________
 |
| A Mancala board with "stones." |
When I was a kid, I used to love to play this African game we called “Kai”. I now know it has many names, most commonly "Mancala." It’s a game played with a carved wooden board and marbles. Or stones. Or shells. Or even seeds. There are many versions of how to play Mancala; we played a game closely resembling this one. [Michael; Kasao, Ghana]
What I loved about the game was the way the pebbles felt in my hands. The dropping of them one by one has a tangibility and a logic and a rhythm of its own (one-to-one correspondence). The heft of a handful of pebbles, the gradual diminishment as you repeatedly subtract one from the handful (subtraction as loss, as “less;” division as repeated subtraction), the gradual addition to each well on the board, the estimation or mental math of knowing how many pebbles are in each well as they change throughout the play (subitizing, number sense). It may have been Math but it was a Math I understood with my hands. No equations or formulae. No pencil or paper. Just doing it. Just replicating a pattern or formula or a simple set of rules, over and over again.
____________________________________
A few years ago, I bought a couple of Mancala boards for my first grade classroom, but the pebbles quickly got lost or used for other activities, the boards got used for sorting trays, and — for one reason or another — it fell off my agenda. I’m wondering now if that was a missed opportunity. And I’m wondering: if I made a Mancala board out of an egg carton — and cut it down to ten wells instead of the traditional twelve, and put five stones in each well…. Now the kids would be playing Mancala in a ten frame. And if we decided that five stones in a well was the number you had to have to “capture” the stones, then we would be working with the numbers that are the basis of our number system and our curriculum. And our hands. (Five fingers per hand, ten in all.)
And it would be like planting seeds. A simple, everyday, organic, radical way of knowing. With our hands.

No comments:
Post a Comment